Geometry¶
The afem.geometry package provides entities and tools for the creation and
use of what is commonly referred to as “construction geometry” or “reference
geometry” for both 2-D and 3-D domains. This package primarily wraps a number
of OpenCASCADE native types and tools in order to provide a more “Pythonic”
user interface. The entities and tools in the geometry package do not cover
every OpenCASCADE type, but rather those frequently encountered during regular
use. The entities and tools can be imported by:
from afem.geometry import *
Geometry entities cover general types like points, curves, planes, and
surfaces. Tools exists for the creation, modification, intersection, and
projection of the geometric entities. The simple example below demonstrates
some of the key entities and tools of the geometry package:
from afem.geometry import *
from afem.graphics import Viewer
gui = Viewer()
# Create a point directly from the entity. Default is (0, 0, 0).
p1 = Point()
# Create a point by array-like
p2 = PointByArray([5, 0, 5]).point
# Create a point by x-, y-, and z-coordinates.
p3 = PointByXYZ(10, 0, 0).point
# Interpolate the points with a curve
c1 = NurbsCurveByInterp([p1, p2, p3]).curve
gui.add(p1, p2, p3, c1)
gui.start()
# Copy curve and translate
c2 = c1.copy()
c2.translate((0, 10, 0))
gui.add(c2)
gui.start()
# Copy and translate again
c3 = c2.copy()
c3.translate((0, 10, 10))
gui.add(c3)
gui.start()
# Approximate a surface
s1 = NurbsSurfaceByApprox([c1, c2, c3]).surface
gui.add(s1)
gui.start()
# Extract an iso-curve
c4 = s1.u_iso(10.)
gui.add(c4)
gui.start()
# Create points along the curve
pnts = PointsAlongCurveByDistance(c4, 1.).points
gui.add(*pnts)
gui.start()
# Extract iso-curve
c5 = s1.v_iso(0.5)
gui.add(c5)
gui.start()
# Intersect two curves
cci = IntersectCurveCurve(c4, c5)
gui.clear()
gui.add(c4, c5, s1, *cci.points)
gui.start()
# Define a plane along a curve
pln = PlaneFromParameter(c4, 0., 2.).plane
# Intersect a surface and a plane
ssi = IntersectSurfaceSurface(s1, pln)
gui.add(s1, *ssi.curves)
gui.start()
# Project a point to a surface
p4 = pln.eval(5, 5)
proj = ProjectPointToSurface(p4, s1)
line = NurbsCurveByInterp([p4, proj.nearest_point]).curve
gui.add(p4, proj.nearest_point, line)
gui.start()
The entities, tool, and viewing tool are imported by:
from afem.geometry import *
from afem.graphics import Viewer
The first variable created is a Point and is constructed directly
from the entity itself. Since the Point class is derived from the
OpenCASCADE type OCCT.gp.gp_Pnt, one of the available constructor methods
is using three floats to define an x-, y-, and z-coordinate. By default the
location is (0., 0., 0.):
p1 = Point()
Points can also be created using a variety of tools including by an array or specified x-, y-, and z-coordinates. When tools are used the underlying entity must be retrieved from the tool by:
p2 = PointByArray([5, 0, 5]).point
p3 = PointByXYZ(10, 0, 0).point
A cubic curve can be created by interpolating points by:
c1 = NurbsCurveByInterp([p1, p2, p3]).curve
Most geometry types can be copied and a limited number of transformations can be directly applied to the entity depending on its type:
c2 = c1.copy()
c2.translate((0, 10, 0))
Here, a new NurbsCurve was created and then translated in the
y-direction by 10 units. This new curve is then copied again and translated in
both the y- and z-directions by 10 units each:
c3 = c2.copy()
c3.translate((0, 10, 10))
These three curves are then used to approximate a NurbsSurface:
s1 = NurbsSurfaceByApprox([c1, c2, c3]).surface
Isoparametric curves (i.e., isocurve) can be extracted from surfaces in both the u- and v-directions. Below, an isocurve is extract at a constant u=10:
c4 = s1.u_iso(10.)
This isocurve is used to generate evenly spaced points using a target distance of 1 unit:
pnts = PointsAlongCurveByDistance(c4, 1.).points
The PointsAlongCurveByDistance tool can also return the number of
points created, the parameters on the curve for each point, the final spacing,
and the interior points (i.e., exclude first and last). Others tools exist for
creating points (and planes) along curves by a specified number rather than
distance.
At this point the created geometry should look similar to the image below.
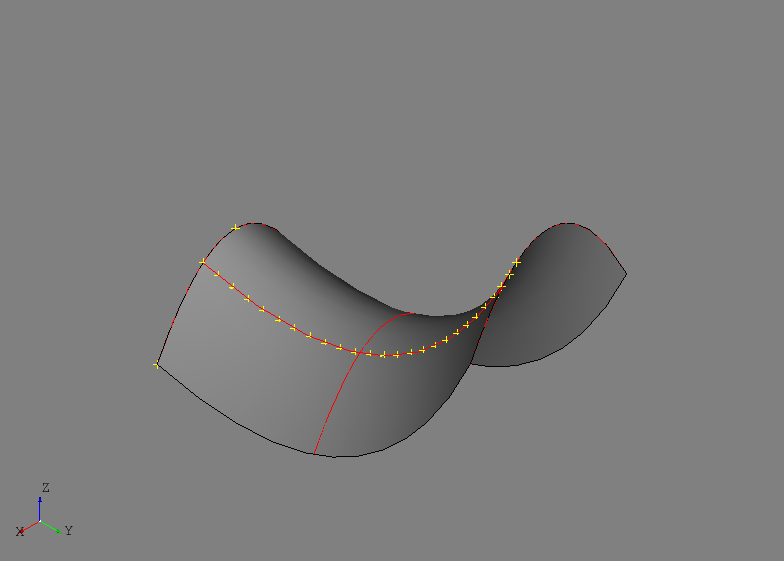
Another isocurve in the opposite direction is created and the intersection is found by:
c5 = s1.v_iso(0.5)
cci = IntersectCurveCurve(c4, c5)
The IntersectCurveCurve tool provides intersection results including
the point(s), parameter(s) on each curve, and number of intersections. Other
tools exist for curve/surface and surface/surface intersections. Intersecting a
plane and a surface is shown by:
pln = PlaneFromParameter(c4, 0., 2.).plane
ssi = IntersectSurfaceSurface(s1, pln)
A Plane is first created using the PlaneFromParameter tool
and then used in the IntersectSurfaceSurface tool. The resulting
intersection curves are approximated in 3-D space.
Projections to curves and surfaces are available using the projection tools. By default, projections are usually performed normal to the curve or surface, but some tools always projections along a specified direction. This operation actually becomes a curve intersection operation rather than a normal projection. The code below creates a point on a plane and then performs a normal projection to the surface:
p4 = pln.eval(5, 5)
proj = ProjectPointToSurface(p4, s1)
line = NurbsCurveByInterp([p4, proj.nearest_point]).curve
The line variable is created mostly for visualization purposes and to
demonstrate some of the data that can be retrieved from the
ProjectPointToSurface tool. All point projection results are stored
in the tool and sorted by minimum to maximum distance.
The intersection and projection results should look similar to the image below. Note that there are no renderings for infinite planes.
